En esta entrada se describe un estudio teórico de cómo se comportan los gases dentro de un horno por lo que se introducen ciertas fórmulas de física como la «ecuación general de los gases» o el «teorema de Bernoulli», etc..
Para simplificar el estudio teórico vamos a considerar que la densidad del aire mezclado con gases y humos es la misma densidad que tiene el aire limpio a 20°C y a la altura del nivel del mar, lo cual es una aproximación razonable. Esta densidad es 1,2 kg/m3
En todos los cálculos, asumimos que la presión atmosférica en el exterior del horno es de 1 atmósfera (101.325 pascales) y la temperatura es de 20ºC.
Dentro del horno tenemos nuestro gas que es aire seco, el cual ocupa todo el volumen interno del horno (V), ejerciendo una presión (P) contra las paredes. Este aire tendrá una temperatura (T) que cambiará según las resistencias o la combustión produzcan calor. La cantidad de moléculas de aire que se encuentran dentro del horno podemos dimensionarla calculando el número de moles (n).
Todas estas variables se relacionan entre sí mediante la ecuación general de los gases que es la siguiente:
P · V = n · R · T
donde R es una constante. Para trabajar con esta fórmula, la presión debe medirse en atmósferas, la temperatura en Kelvin (K = ºC + 273) y el volumen en m3.
Si consideramos que el horno es un recipiente hermético, el volumen V es invariable y los moles de aire contenidos en el interior no cambian, por lo que, despejando en la ecuación anterior obtenemos la ley de Gay Lussac que se expresa de la forma siguiente:
P / T = constante
dicho de otra forma, para temperaturas T1, T2, T3 tendremos la siguiente igualdad:
P1 / T1 = P2 / T2 = P3 / T3
Y así podríamos calcular la presión para distintas temperaturas de este horno hipotético en el que no hay entrada ni salida de aire, obteniendo los siguientes resultados teóricos:
- para 20ºC (horno apagado) la presión es 1 atmósfera
- para 100ºC obtenemos 1,27 atm
- para 1000ºC la presión es 4,34 atm
- para 1250ºC la presión es 5,37 atm
Este cambio de presión con la temperatura se debe a que las moléculas del gas, en este caso aire, aumentan su vibración y su energía interna con el calor, chocando un mayor número de veces contra las paredes del horno, produciendo así una mayor presión.
La presión llega a ser tan grande, que nuestro horno hermético hipotético podría agrietarse o romperse, al igual que puede ocurrir con las ollas a presión.
Pero los hornos no son recipientes herméticos sino que disponen de orificios destinados a la entrada y salida de aire y gases. Debido a la existencia de estos orificios, al aumentar la temperatura, el aumento de vibración de las moléculas hace que ocupen más espacio cada una (expansión del gas) de forma que algunas moléculas escapan del interior del horno. El resultado es que dentro del horno el aire tiene menor densidad, es decir quedan menos moléculas cuanto mayor es la temperatura.
Esto equivale a decir que el peso específico del aire disminuye al calentarse. El peso específico es el peso por unidad de volumen y es igual al producto de la densidad (del aire en este caso) por la aceleración de la gravedad.
Ɣ = ρ · g
Esto también podemos verlo en la ecuación general de los gases si hacemos algunos cambios…
Por un lado, sabemos que el número de moles “n” es igual a la masa dividido por la masa molecular (por ejemplo, como la masa molecular del oxígeno (O2) es 16 + 16 = 32, si tenemos 5 gramos de moléculas de oxígeno tendremos 5 / 32 = 0,156 moles).
Por otro lado, también sabemos que la densidad (ρ) es igual a la masa dividido por el volumen.
n = m / Mmol ρ = m / V
Por lo que la ley general de los gases también puede formularse así:
P · Mmol = ρ · R · T
Cuando consideramos nuestro horno con orificios de entrada y salida de aire ya no podemos decir que el volumen es constante. Sin embargo sí podemos considerar que la presión se mantiene constante y en este caso obtenemos la siguiente expresión:
ρ · T = constante
De esta forma podemos hacer un cálculo teórico de la densidad del aire en el interior del horno para distintas temperaturas. ya que siempre se va a cumplir que el producto de densidad por temperatura tiene el mismo valor. Por ejemplo, podemos comparar lo que ocurre dentro y fuera del horno con la siguiente igualdad:
ρext · Text = ρint · Tint
Si suponemos que fuera del horno estamos a una temperatura ambiente de 20ºC (o sea 293 Kelvin) y con una densidad del aire de 1,2 Kg/m3, tendremos:
- Para horno apagado (20ºC = 293 K): ρint = 1,2 · 293 / 293 = 1,2 Kg/m3
- Para una temperatura de 100ºC = 373 K: ρint = 1,2 · 293 / 373 = 0,943 Kg/m3
- Para una temperatura de 1000ºC = 1273 K: ρint = 1,2 · 293 / 1273 = 0,276 Kg/m3
- Para una temperatura de 1250ºC = 1523 K: ρint = 1,2 · 293 / 1523 = 0,231 Kg/m3
Dependiendo del tipo de fuente de calor del horno, la densidad del gas será más o menos homogénea. Mientras que en los hornos eléctricos las resistencias se reparten por toda la superficie de las paredes del horno, en los hornos de combustión, las fuentes de calor están situadas en la parte inferior del horno lo que se traduce en mayores diferencias de densidad entre el aire cercano a los quemadores (o al hogar) y el aire más alejado de esas fuentes de calor.
Como ya se dijo al comienzo de esta entrada, no se tienen en cuenta en estos cálculos los cambios de densidad debidos a la presencia de los gases de combustión y otros gases generados durante la cocción, ni los cambios en la densidad del aire motivados por la humedad o la altura respecto al nivel del mar.
En cualquier caso, este cambio de densidad de los gases contenidos en el interior del horno en función de la temperatura es el responsable del sistema de ventilación natural que se produce en los hornos, que suele denominarse “efecto chimenea”.
El aire menos denso, con menor peso específico, tiende a subir hacia la parte superior del horno, creándose así un flujo o corriente de aire/gas. Entra aire frío por el/los orificios situados en la parte inferior del horno y sale aire y otros gases calientes por la parte superior del horno.
El principio de Bernoulli explica los flujos de un fluido (un gas en nuestro caso), y nos dice que la suma de todas las energías del fluido permanece constante a lo largo del flujo. Las energías del fluido son su presión (energía interna producida por la vibración, rotación y traslación de las moléculas del gas), su energía cinética (consecuencia de su velocidad de desplazamiento) y su energía potencial (la energía gravitatoria).
Este principio se traduce en la siguiente ecuación:
P + ( ½) ρ v2 + ρ g h = constante
La presión y el resto de variables en la fórmula de Bernoulli deben estar en unidades internacionales. En particular, la presión debe ser medida en pascales (1 atm = 101325 pascales).
Por explicar un poco esta fórmula, se trata de que 3 cosas suman siempre lo mismo. Es decir, si aumenta la energía cinética o la energía potencial significa que la presión disminuye. O lo que es lo mismo: si aumenta la densidad, la velocidad o la altura entonces la presión disminuye.
El principio de Bernoulli sólo es válido para fluidos en los que las turbulencias, viscosidad, compresión, radiación calorífica, y otros efectos irreversibles son muy pequeños o despreciables (entropía constante). Para simplificar nuestro análisis consideramos que el gas contenido en el horno es así.
Vamos a hacer algunas consideraciones para que la fórmula de Bernoulli sea lo más sencilla posible…
Podemos decir que el aire en el interior del horno es estático y no tiene movimiento, es decir, la velocidad del aire en el interior del horno es tan pequeña que la energía cinética puede considerarse despreciable. La ecuación de Bernoulli simplificada, para el interior del horno, quedaría así:
P + ρ g h = constante
La energía potencial de los gases en nuestro horno depende de la diferencia de los pesos específicos del aire que está dentro y fuera del horno. Es decir, el comportamiento es igual al de los vasos comunicantes.
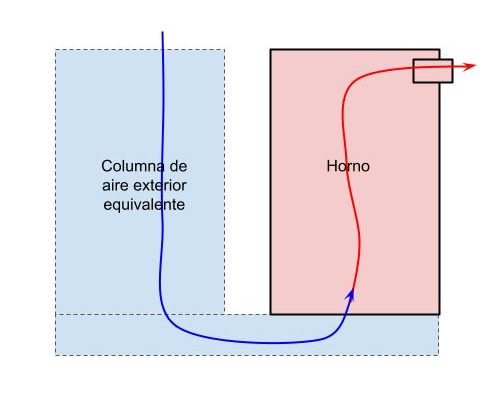
El aire que está en el exterior del horno, con mayor densidad y mayor peso, empuja al aire que está en el interior del horno que es más liviano porque está más caliente.
Si escogemos un punto B situado en la base del horno y consideramos que está a una altura cero y un punto C situado en la parte superior del horno a una altura H, según Bernoulli podemos decir:
PB = PC + (ρext g H – ρint g H)
En la fórmula anterior, la energía potencial en la parte alta del horno es igual al peso específico de una columna de aire frío de altura H menos el peso específico de la columna de aire caliente de altura H (vasos comunicantes).
Como podemos ver en la fórmula anterior, la presión en el punto B (abajo) es mayor que la presión en el punto C (arriba) y esa diferencia de presión es:
ΔP = PB – PC = (ρext – ρint) g H
Esa depresión o diferencia de presiones (ΔP) es la responsable del llamado “efecto chimenea”, que consiste en la formación de un flujo o movimiento de los gases que se desplazan desde la zona de más presión a la zona de menor presión. Ese flujo continúa hasta lograr el equilibrio (que se alcanza cuando las presiones son iguales).
Frente a la presión atmosférica, que podemos considerar que es igual a una atmósfera, es decir, 101325 pascales, el efecto chimenea en un horno se debe a depresiones de alrededor de 20 pascales. Estas cifras nos dan una idea de lo delicado que es este proceso natural que puede ser anulado por cualquier anomalía en el circuito de ventilación/evacuación.
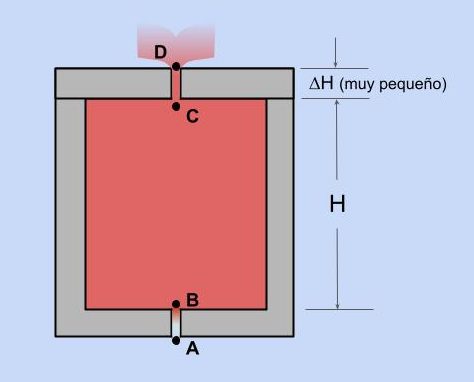
La depresión que se produce en el interior del horno hace que se produzca la salida de aire/gas caliente por el orificio de salida a una velocidad determinada.
Si consideramos un punto D justo a la salida del horno, considerando que la altura del punto D es prácticamente igual a la altura del punto C, tenemos con Bernoulli:
PC = PD + ½ ρint vs2
La presión en el punto D es menor que la presión en el punto C ya que aparece la energía cinética con la velocidad “vs” de salida de gases. Despejando tenemos que:
PC – PD = ½ ρint vs2
Es decir, la depresión producida por el efecto chimenea entre los puntos B y C se traduce en la salida de gases a velocidad “vs”.
Podemos decir que:
PB – PC = PC – PD
Y por tanto:
(ρext – ρint) g H = ½ ρint vs2
Despejando la velocidad obtenemos:
vs = √[2·g·H· (ρext – ρint )/ ρint]
Podemos hacer los mismos razonamientos si consideramos un punto A situado en la entrada de aire del exterior y obtendremos:
PA – PB = PB – PC
½ · ρext · ve2 = (ρext – ρint) · g · H
ve = √[2·g·H· (ρext – ρint )/ ρext]
La velocidad de entrada de aire frío es inferior a la velocidad de salida de aire caliente en función del ratio entre las densidades del aire interior y exterior.
Podríamos decir que el número de moléculas por segundo (el flujo molar) es igual a la entrada y a la salida del horno. A la entrada, con mayor densidad se necesita menor velocidad que a la salida, donde la densidad es menor.
Por tanto, podemos decir que las partículas de aire contenidas en el horno llegan a la parte superior del horno de forma que algunas de ellas saldrán directamente por el orificio de salida del horno mientras que otras chocarán con la parte de arriba del horno modificando su dirección.
Los hornos de tiro invertido y de tiro cruzado tienen el orificio de salida en la parte inferior del horno y se construyen haciendo una bóveda en la parte superior del horno. Estos hornos son de combustión y en ellos los humos calientes suben hacia la bóveda intentando salir al exterior pero, al no encontrar ningún orificio, la velocidad de salida va modificando su dirección hasta que comienza a descender y encuentran una zona de menor presión que es donde se encuentra el orificio de salida a la chimenea.
El caudal volumétrico (Q) en un flujo de fluidos es el volumen de fluido que pasa por una sección determinada por unidad de tiempo.
El caudal (Q) es el producto de la velocidad del fluido por el área o sección del ducto por el que pasa dicho fluido:
Q = (Área) x (velocidad) = A·v
El tamaño de los orificios de entrada y salida de aire y gases en el horno no deben ser demasiado grandes ya que se perdería mucho calor, pero con tamaño suficiente para que el aire y los gases se renueven cada cierto tiempo. En los hornos de combustión, además, se necesita mucho oxígeno para que se pueda realizar la combustión, por lo que es necesaria una renovación del aire más rápida para su correcto funcionamiento en atmósfera oxidante.
En todo este proceso que se produce en el horno hay pérdidas de carga debidas principalmente a la disipación térmica a través de las paredes del horno, el rozamiento del aire y los gases con las rugosidades, etc. Todas estas pérdidas se reflejan en el valor del caudal y por ello se suele añadir un parámetro denominado “coeficiente de descarga” (C) que es un factor corrector para que el cálculo del caudal esté más próximo a la realidad. El valor de este coeficiente disminuye en función de las turbulencias, fricciones, etc..
Q = A · C · v
Hasta aquí hemos visto lo que ocurre dentro del horno, pero ¿ qué ocurre después ?
El aire caliente que procede del horno, tras atravesar el orificio de salida, entra en una conducción (tubería metálica, de ladrillos, etc..), que dirige el caudal de aire y gases hasta el exterior. Este conducto se denomina chimenea en los hornos de combustión, pero en los hornos eléctricos suele denominarse tubo de evacuación o de ventilación.
La base de este conducto o chimenea debe estar abierta, es decir, la conexión horno-chimenea no es un tubo sellado sino abierto al aire del ambiente.
En la chimenea o tubo de evacuación se vuelven a producir los mismos procesos físicos que se han descrito para el interior del horno. El llamado “efecto chimenea” se vuelve a producir, pero con una diferencia importante que es la ausencia de las fuentes de calor del interior del horno. Es decir, en la chimenea el aire caliente de su interior (procedente del horno) se va enfriando según avanza en su recorrido ascendente en función de las pérdidas de carga.
Mientras que en el interior del horno las pérdidas de calor se compensan con un mayor consumo de leña, gas, o electricidad, en la chimenea las pérdidas de carga debidas a disipación térmica, rozamientos de los gases con las rugosidades, y pérdidas debidas codos, cambios de dirección, registros, etc.. se traducen en la pérdida de temperatura y pérdida de velocidad de salida de los gases.
Por este motivo, es importante saber a qué temperatura ingresan los gases procedentes del horno en la base de la chimenea.
Cuando salen del horno, los gases están a la temperatura del horno pero, inmediatamente, al verse liberados de las paredes que los contienen, se expanden rápidamente disminuyendo su energía interna y disminuyendo notablemente su temperatura.
Esta expansión se denomina expansión adiabática y la bajada de temperatura que se produce obedece a la fórmula:
Tfinal = Tinicial ·(Pfinal / Pinicial)(૪-1) / ૪)
Donde ૪ es el coeficiente de dilatación adiabática que, para el aire seco, tiene valores que oscilan entre 1,4 (a 20ºC), 1,401 (a 100ºC), 1,365 (a 1000ºC) y 1,3 (a 1250ºC). Las temperaturas deben estar en Kelvin y las presiones en atmósferas en esta fórmula.
Considerando que la presión inicial en la fórmula anterior es igual a la presión interior del horno para cada temperatura, y que la presión final que se llega a alcanzar es aproximadamente 1 atmósfera, tenemos en nuestro caso:
Tfinal = THorno ·(1 / PHorno)(૪-1) / ૪)
Si hacemos este cálculo obtenemos que para temperatura del horno de 1000ºC el aire expandido rebaja su temperatura a 600ºC, y para una temperatura de 1250ºC en el horno se queda en 760ºC aproximadamente.
Además de la expansión adiabática, el aire caliente se mezcla y se diluye en el aire a temperatura ambiente de forma que su temperatura se rebaja todavía más.
El resultado es que el aire y los gases calientes procedentes del horno llegan a la chimenea a temperaturas por debajo de los 300ºC y comienzan a ascender debido a la depresión ascendente que hemos llamado “efecto chimenea” y que tiene el valor:
ΔP = (ρext – ρint) g HChim
Al igual que en el interior del horno, esta depresión depende de la diferencia entre densidades (ρext – ρint) y de la altura.
En la construcción de hornos, aumentar la altura del horno es un problema desde el punto de vista de eficiencia energética por lo que el “efecto chimenea” se produce principalmente por la gran diferencia de temperaturas que hay entre el interior y el exterior del horno.
Sin embargo, en las chimeneas, la diferencia de temperatura entre el interior y el exterior es mucho más pequeña por lo que el “efecto chimenea” se logra con la altura.
Si consideramos que la chimenea funciona como los vasos comunicantes, el aire exterior forma la columna de aire frío con un peso superior a la columna de aire caliente del interior de la chimenea. Cuanto más alta es la chimenea, más alta será también la columna equivalente exterior de aire de forma que habrá más peso que empuje el aire que hay dentro de la chimenea.
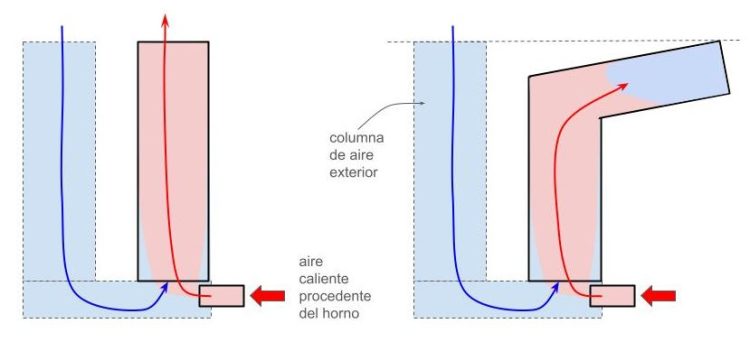
El peso del aire caliente que se encuentra dentro de tramos horizontales o inclinados de una chimenea, no se compensa con más aire frío y pesado del exterior ya que la altura de la chimenea no cambia o cambia muy poco. Por este motivo deben evitarse estos tramos horizontales al mínimo imprescindible y compensarlos con una mayor altura de la chimenea vertical.
Una presión ascendente mayor implica una mayor velocidad de salida del aire hacia el exterior, que es realmente lo que se busca con la chimenea. Recordemos que la velocidad de salida del aire es:
vC = √(2·ΔP / ρchim)
Hasta aquí parece evidente que las chimeneas cuanto más altas mejor, pero no es del todo cierto ya que cuanto mayor es la altura mayores son las “pérdidas de carga”.
Podemos clasificar las distintas “pérdidas de carga” en tres categorías:
- Pérdidas por dispersión térmica: Las paredes de la chimenea absorben calor y la temperatura del aire y gases disminuye. Este enfriamiento depende, en gran medida, de la conductividad térmica de los materiales con los que se han construido la chimenea y el aislante empleado. Pero también depende de la diferencia de temperatura que hay entre el interior y el exterior de la chimenea, de la altura y del diámetro de la chimenea (a mayor superficie mayor enfriamiento) y de la velocidad de los humos (a mayor velocidad menos pérdidas).
Una chimenea de chapa sin aislante en la que ingresan gases a 200ºC por su base rebajará su temperatura a 110ºC al alcanzar 1 metro de altura, y llegará a 60ºC tras alcanzar 2 metros de altura. Pero si la chapa está recubierta por una buena capa de material aislante, estas pérdidas por calor se reducen enormemente.
- Pérdidas por rozamiento: El rozamiento de aire/gases con las paredes de la chimenea reduce la velocidad. El rozamiento es directamente proporcional a la rugosidad de las paredes y al cuadrado de la velocidad de los humos, además, depende de la forma del conducto y su longitud.
Esto significa que reduciendo la velocidad de los gases en la chimenea (por ejemplo aumentando su sección “n” veces) se disminuyen en gran medida las pérdidas por rozamiento (n2 veces).
- Pérdidas por obstáculos: Obstáculos como curvas, codos, registros, estrechamientos y ensanchamientos de la sección, etc. siempre producen caídas en la presión ascendente.
En una chimenea recta y bien aislada, podemos decir que las pérdidas de carga son mayoritariamente debidas al rozamiento, es decir, inversamente proporcionales al cuadrado del diámetro de la chimenea.
En resumen, cuanto más alta es la chimenea es mayor la presión ascendente (mayor velocidad), y cuanto mayor sea su sección menores serán las pérdidas, pero será necesaria mayor energía calorífica para mantener la temperatura de los gases. Una chimenea alta necesita menor sección mientras que una chimenea baja necesita mayor sección.
En general las chimeneas trabajan con depresiones entre 8 y 13 pascales que se quedan en un valor menor si se tienen en cuenta las pérdidas de carga. La velocidad de salida de los gases de la chimenea suele estar entre 1,5 m/s y 6 m/s.
El efecto chimenea suele tener muy poco tiro en bajas temperaturas. Si el horno es de combustión el problema es todavía mayor porque se generan muchos gases y humos que absorben mucho aire frío que enfría la temperatura.

Un comentario en “El «efecto chimenea»”