Dentro de la cerámica, el efecto Venturi es conocido porque ayuda a la salida de humos de la chimenea y al circuito de ventilación del horno. Cuando hay una suave brisa en el exterior, nuestro horno funciona mucho mejor y los gases y el aire caliente salen sin ninguna dificultad.
Además, el efecto Venturi es necesario para tener «sistemas de ventilación forzada por corriente descendente», o para que trabajen los aerógrafos y las pistolas de pintura, o incluso para poder refrigerar nuestro taller sin utilizar aire acondicionado.
Bernoulli estableció que, en el flujo de un fluido, siempre se mantiene constante la suma de la presión, de la energía cinética provocada por la velocidad, y de la energía potencial provocada por la altura.
Si suponemos que no hay variaciones en la altura, el teorema de Bernoulli se simplifica y nos dice que la presión disminuye cuando aumenta la velocidad del fluido (y viceversa). En realidad, como la velocidad tiene dirección y sentido, «aumentar la velocidad» significa mayor velocidad en el sentido del flujo.
Si el aire en el exterior de la chimenea está en movimiento con una dirección y sentido similar a la salida de la chimenea o, como máximo, perpendicular a la chimenea, se produce una succión de los gases que salen debida al «efecto Venturi». Es decir, el viento produce una depresión adicional a la depresión provocada por el efecto chimenea.
Hagamos algunos cálculos para concretar valores:
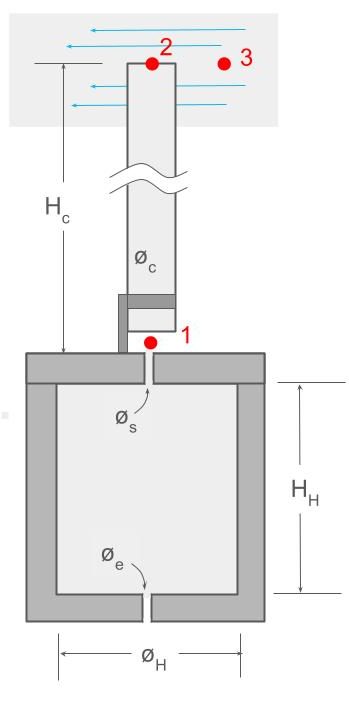
En la anterior figura se representa un horno cerámico con su chimenea y hemos seleccionado los puntos 1, 2 y 3 para ver como el efecto Venturi refuerza el efecto chimenea.
Sabemos que la presión en la parte inferior de la chimenea P1 es mayor que la presión en la parte superior de la chimenea P2 y por ello el aire sube.
Por otro lado, para que el humo pueda salir de la chimenea, la presión fuera debe ser más pequeña que la presión dentro de la chimenea, o sea: P3 < P2 → P2 – P3 > 0
Como no sabemos cual es el valor de P2 – P3, podemos hacer una conjetura y suponer que P2 – P3 = P1 – P2 . Si esta igualdad se cumple, es seguro que el humo saldrá de la chimenea sin ningún problema. Por el efecto Chimenea, sabemos que esta diferencia de presiones es:
P1 – P2 = (ρext – ρC ) g HC
siendo ρext la densidad del aire en el exterior, ρC la densidad del aire en el interior de la chimenea y HC la altura de la chimenea.
por tanto:
(ρext – ρC ) g HC = P2 – P3
También sabemos que P3 es la presión atmosférica (101.300 pascales) en ausencia de viento, por lo que:
P2 = (ρext – ρC )·g·HC + P3
O sea, el valor obtenido de P2 siempre es superior a 101.300 pascales (que es el valor de la presión atmosférica en ausencia de viento) y nuestra chimenea funcionará correctamente en ausencia de viento.
Ahora analizamos lo que ocurre cuando hay viento (efecto Venturi).
Si a la salida de la chimenea el aire se mueve con velocidad Vv, la presión P3 ya no será la presión atmosférica (Patm = 101.300 pascales), sino un valor más pequeño:
P3 = Patm – (½) · ρext · Vv2
En consecuencia, la diferencia de presiones P2-P3 será mayor, por lo que aumenta la velocidad de salida de los gases de la chimenea.
Si el viento tuviese una velocidad con trayectoria inclinada hacia el suelo se introduciría por la chimenea y se produciría un tiro negativo que impediría la salida del aire caliente del horno.
El efecto Venturi es también el responsable del funcionamiento de los “sistemas de ventilación forzada de corriente descendente”, utilizados en hornos eléctricos, que consisten en generar una depresión en la base del horno mediante una corriente de aire generada por un extractor o turbina.
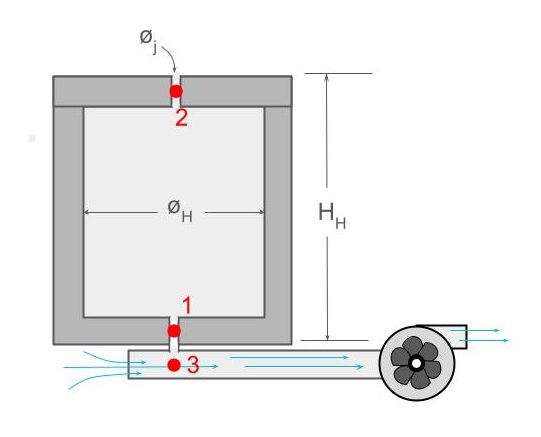
En la figura aparece el esquema de un horno al que hemos acoplado una turbina por la parte inferior. Vamos a suponer que esa turbina extrae un caudal de aire QT
La turbina se conecta a un tubo con un diámetro ØT, que pasa por debajo del horno al que se une a través de un agujero bastante estrecho. El efecto Venturi va a hacer que la corriente de aire que genera la turbina extraiga el aire del interior del horno a través de ese pequeño agujero que los une.
La pregunta principal para el diseño de estos sistemas es calcular el diámetro del agujero de salida del horno, para una turbina con un caudal de extracción determinado (QT) conectada a un tubo de extracción de diámetro conocido (ØT).
Para un diámetro de tubo ØT, es decir, con radio rT, el área del tubo AT será:
AT = π · rT2
También podemos calcular la velocidad del aire en el interior del tubo, que será:
vT = QT / AT
Si la diferencia de presión debida al “efecto chimenea” entre la parte alta del horno (P2) y la base del horno (P1) es:
P1 – P2 = (ρext – ρint) g HH
Para conseguir una corriente de aire en sentido inverso necesitamos ahora que la presión en el punto 2 (arriba) sea superior a la presión en el punto 1 (abajo), es decir:
P2 – P1 > (ρext – ρint) g HH
Si consideramos un punto 3 situado en el tubo de extracción de aire, justo debajo de los puntos 1 y 2, necesitamos que en ese punto la presión sea todavía más baja para que se produzca la extracción de aire.
Por ejemplo, si decimos que:
P3 – P1 = P2 – P1 > (ρext – ρint) g HH
Tendremos la corriente descendente asegurada. Hacemos cálculos aplicando Bernoulli y considerando que los puntos 1 y 3 están prácticamente a la misma altura y tenemos:
P3 + (½) · ρext · vT2 = P1 + (½) · ρint · vS2
P3 – P1 = (½) · ρint · vS2 – (½) · ρext · vT2
Por tanto podemos calcular la velocidad de salida del aire desde el interior del horno vj
vj > √ {[ 2gHH (ρext – ρint) / ρint ] + (ρext · vT2 / ρint)}
Además, el caudal que sale del horno debe ser parecido al caudal del horno cuando funciona con el “efecto chimenea”. Si fuese un caudal demasiado grande podría bajar mucho la eficiencia del horno ya que se enfriaría demasiado.
Por tanto:
rs2· √[2·g·HHorno· (ρext – ρint )/ ρint] = rj2· √ {[ 2gHH (ρext – ρint) / ρint ] + (ρext · vT2 / ρint)}
Y de esta forma queda determinado el radio (y el diámetro) de los orificios de entrada y salida de gases necesarios para el sistema de corriente invertida.
rj4 = [rs4·2·g·HH·(ρext – ρint)/ ρint] / {[2gHH (ρext – ρint)/ρint ] + (ρext·vT2/ρint)}
Veamos un caso práctico. Si nos compramos una turbina con caudal de extracción de 124 m3/hora (o lo que es lo mismo 0,03445 m3/seg) y la conectamos a un tubo flexible que tiene un diámetro interior de 5 cm, podemos calcular la velocidad a la que circula el aire por dentro del tubo vT
vT = QT / AT = 0,03445 / (π · 0,0252 ) = 17,5 m/seg
Calculamos también la velocidad del aire de salida del horno que necesitamos (vj ) . Hacemos los cálculos para una temperatura bastante alta, por ejemplo 1250°C, por lo que la densidad del aire en el interior del horno sería ρint = 0,231 kg/m3. Con estos datos obtenemos vj > 40,46 m/seg
Y ahora calculamos el radio de los orificios de entrada y salida que necesitamos en el horno para que el caudal sea el mismo que el que hay con el efecto chimenea y obtenemos
rj = 0,003 m
Es decir, necesitamos agujeros de 6 mm de diámetro.
Como puede verse, se necesitan agujeros muy estrechos. Por eso, estos sistemas de ventilación requieren que se tapone la salida y la entrada que vienen de fábrica con el horno para realizar a continuación nuevos agujeros de entrada y salida con una broca y con unos pocos milímetros de grosor (6 mm en nuestro ejemplo).
Y así tenemos nuestro sistema de ventilación por corriente descendente. Naturalmente, si cambian los valores del caudal de la turbina o del diámetro del tubo por donde circula el aire también cambiará el diámetro de los agujeros que hay que realizar en el horno.

Un comentario en “El efecto Venturi en los hornos”